|
Expressions are one of messiah's most useful and
powerful features, but many people get intimidated by the math that
may be involved. Short expressions are easy to understand,
such as: [Foot.lwo:xpos]*3 which will take the X
position of Foot.lwo and
multiply it by 3.
Unfortunately, many expressions are more complex than
that. While it might take a book or full class to explain
everything (and if you are planning something like that, let me
know because I'll sign right up), here is a quick look at how they
break down, and what it all means.
Objects and Channels:
The first, and most basic thing to know is that objects and their
channels get placed into brackets ( [
] ), and that no other part of the expression goes in
there. For example, [Foot.lwo:xpos] is correct, but [Foot.lwo:xpos+2] is not.
If you want to add 2 to the X position of
Foot.lwo, the +2
belongs outside the brackets, like this: [Foot.lwo:xpos]+2
There is an exception though. This is a perfectly
legitimate format: [Null:xpos@ etc. ]
For example: [Box.lwo:xpos@[Slider:xpos]*10+25]
Technically, that's still
presenting an object an channel-- it's just a modified
result.
Common operations:
Here's how each of the basic math operations are written in
expressions...
|
Addition:
|
+
|
(plus sign)
|
|
Subtraction:
|
-
|
(dash)
|
|
Multiplication:
|
*
|
(asterisk)
|
|
Division:
|
/
|
(forward slash)
|
|
Exponent:
|
^
|
(carrot)
|
|
Frown:
|
: (
|
just kidding :-)
|
Comparisons:
One use of comparisons is when you only want something to happen
based on the relation of one number to another. Like if the
Y position of object A is greater than 2.5,
make object B follow it.
Greater
than:
>
Less
than:
<
Equal
to:
=
Greater than or equal to: >=
Less than or equal to:
<=
Less than or equal to or just about the same but not
really: <=~=x
Order of
operations:
Here's a quick look at the order in which simple equations get
solved in:
-
Parentheses (functions have the same level of precedence as
parentheses)
-
Exponents
-
Multiply
(or divide)
-
Add (or
subtract)
Here are
some easy samples:
-
3+2*5= 13 The multiplication happens
first. 2*5=10, then 10+3=13. The wrong answer would be 25 (which you'd
get by adding 3+2 then multiplying by 5).
-
3+2*5+4=
17 Again,
the multiplication happens first, so the equation is
actually: 2*5=10, then 10+3+4= 17.
-
(3+2)*5=
25 The
parentheses happen first. So the equation is
3+2=5, then 5*5=25.
-
(3+2)*(3+2)=
25 Both
parentheses parts are done, then multiplied. So it's
3+2=5, then
another 3+2=5, then 5*5=25.
The complex expression:
OK, that was all pretty easy. Now lets dive right into a long
and complex equation. (This equation is from a complex
character setup.)
[Hip:xpos]*(1-(abs([HipSld:xpos]-.5)*2))+[FtL_CTL:xpos]*(max([HipSld:xpos],.5)*2-1)+[FtR_CTL:xpos]*(abs((min([HipSld:xpos],.5)-.5))*2)
First
separate it into terms. Terms are separated by addition or
subtraction, and this expression has three terms:
First
term:
[Hip:xpos]*(1-(abs([HipSld:xpos]-.5)*2))
Second
term: +[FtL_CTL:xpos]*(max([HipSld:xpos],.5)*2-1)
Third
term:
+[FtR_CTL:xpos]*(abs((min([HipSld:xpos],.5)-.5))*2)
Now each
of these terms can be broken up (visually anyway) into major
coefficients:
First
term: [Hip:xpos]
*
(1-(abs([HipSld:xpos]-.5)*2))
Second
term: +[FtL_CTL:xpos]
* (max([HipSld:xpos],.5)*2-1)
Third
term: +[FtR_CTL:xpos]
*
(abs((min([HipSld:xpos],.5)-.5))*2)
OK, the
left side of each of these terms evaluates to themselves, they
can't be simplified further. The right side of each of
them can now be simplified according to the order of
operations:
-
Parentheses (functions have the same level of precedence as
parentheses)
-
Exponents
-
Multiply
(or divide)
-
Add (or
subtract)
Let's look
at each term...
The first
term, [Hip:xpos]*(1-(abs([HipSld:xpos]-.5)*2))
works out like this:
[Hip:xpos]*
Hip's X position times the
result of all of the following:
[HipSld:xpos]-.5 HipSld's X position minus
.5
abs
(result)
Take the absolute value of that
result and...
result
*2
Multiply it by
2.
1-
result
Now take 1 and subtract
the result (from above) from it.
Since this
is all modifying the value of HipSld (which is a Slider) you could say that it's
"re-mapping" it's range from 0->1 to 0->1->0. So the
complete term:
[Hip:xpos] * (1-(abs([HipSld:xpos]-.5)*2)) could also
be described as the Hip's
X position times the remapped slider, HipSld.
The second
term, +[FtL_CTL:xpos]*(max([HipSld:xpos],.5)*2-1)
works out like
this:
+[FtL_CTL:xpos]*
FtL_CTL's X position times the result
of:
max([HipSld:xpos], .5) HipSld's X position or .5,
whichever is greater
result *
2
The result of the above, times
2
result
-1
The result of the above minus
1.
This also
remaps the slider. The first half of the sliders range 0->.5
does nothing, it's remapped to 0. The last half .5->1 is
remapped to 0->1.
So now the
first two terms together is: Hip's X position times the remapped
(0->1->0) slider HipSld. That is added to the result of
FtL_CTL's X
position times the remapped (0->0->1) slider HipSld.
The last
term is basically the opposite of the second term,
+[FtR_CTL:xpos]*(abs((min([HipSld:xpos],.5)-.5))*2)
which works out like
this:
+[FtR_CTL:xpos]*
FtR_CTL's X position times the result
of:
min([HipSld:xpos],.5) Returns whichever is smaller; the xpos or
.5.
result
-.5
The
result, minus .5, which makes .5=0 and
0= -.5.
abs (result)
The
absolute value of that result makes it .5=0 and 0
=.5
result *2 This result is then multiplied by 2
(scaling the range) making .5=0 and
0=1.
This
remaps the slider from 1->0->0. In other words the
slider is 1 when it's all the way to the left,
0 when it's in the middle and still 0 at the
far right.
So the
whole thing is:
Hip's X position times the remapped (0->1->0)
slider HipSld. That
is added to the result of FtL_CTL's X position times the remapped
(0->0->1) slider HipSld. The result of that is added to the result of
FtL_CTL's X
position times the remapped (1->0->0) slider HipSld.
And there
you have it. That's how complicated expressions get broken
down and evaluated. However...
Make it a little easier on yourself:
Usually if you have a huge expression like that (or bigger) it's
better to break up the terms into expressions of their own.
Perhaps most common is to break up the remapped sliders into their
own expressions because you tend to use them in more than one
place. (Remember, expressions can be referenced in other
expressions.) The expression detailed above could be
simplified to:
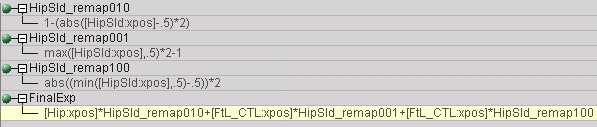
That would
make dissecting it far more easy, especially if you used a naming
convention like "_remap010" to describe what the
expression does rather than leaving it cryptic and
mysterious.
|
